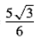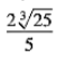NumberofTermsNonnegativeIntegers(2-3x)∛2x-√3Quadratic0≤x≤2Constant24x^2-28x-20VariableBinomial4w^4-25NonnegativeCubicTerminatesb≤6and (-∞,6]4Degreec≥0and[0,∞)y^3+4y^2-3y-12|c+3|≥12AbsoluteValueMonomialy^3+3y^2+3y+1UnboundedTrinomialRadicand. 8x^3-y^3-12x^2y+6xy^2m^2-j^2-8m+165x√3xStandard-x^4True-4x-20BoundedLikeRadicals36-y24y+7DivideLinear-7<d<0and(-7,0)-3<x≤52∛3240y^3+96y^2p-qa^2+2ab+b^2{1, 2,3, 4, 5,....}16x^3+58x^2+22-18z^2+6zIndexRationalx^2+z^2+2xz-1-3<x7{... -3, -2,-1, 0, 1,2, 3, ...}QuarticFOILIrrational“Many”NumberofTermsNonnegativeIntegers(2-3x)∛2x-√3Quadratic0≤x≤2Constant24x^2-28x-20VariableBinomial4w^4-25NonnegativeCubicTerminatesb≤6and (-∞,6]4Degreec≥0and[0,∞)y^3+4y^2-3y-12|c+3|≥12AbsoluteValueMonomialy^3+3y^2+3y+1UnboundedTrinomialRadicand. 8x^3-y^3-12x^2y+6xy^2m^2-j^2-8m+165x√3xStandard-x^4True-4x-20BoundedLikeRadicals36-y24y+7DivideLinear-7<d<0and(-7,0)-3<x≤52∛3240y^3+96y^2p-qa^2+2ab+b^2{1, 2,3, 4, 5,....}16x^3+58x^2+22-18z^2+6zIndexRationalx^2+z^2+2xz-1-3<x7{... -3, -2,-1, 0, 1,2, 3, ...}QuarticFOILIrrational“Many”

Precalculus Prerequisite Bingo - Call List

(Print) Use this randomly generated list as your call list when playing the game. There is no need to say the BINGO column name. Place some kind of mark (like an X, a checkmark, a dot, tally mark, etc) on each cell as you announce it, to keep track. You can also cut out each item, place them in a bag and pull words from the bag.


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
  1. Number of Terms
  2. Nonnegative Integers
  3. (2-3x) ∛2x
  5. -√3
  6. Quadratic
  7. 0≤x≤2
  8. Constant
  9. 24x^2-28x-20
  10. Variable
  11. Binomial
  12. 4w^4-25
  13. Nonnegative
  14. Cubic
  15. Terminates
  16. b≤6 and (-∞,6]
  17. 4
  18. Degree
  19. c≥0 and [0,∞)
  20. y^3+4y^2-3y-12
  21. |c+3|≥12
  22. Absolute Value
  23. Monomial
  24. y^3+3y^2+3y+1
  25. Unbounded
  26. Trinomial
  27. Radicand
  28. . 8x^3-y^3-12x^2 y+6xy^2
  29. m^2-j^2-8m+16
  30. 5x√3x
  31. Standard
  32. -x^4
  33. True
  34. -4x-20
  35. Bounded
  36. Like Radicals
  37. 36-y
  38. 24y+7
  39. Divide
  41. Linear
  42. -7<d<0 and (-7,0)
  43. -3<x≤5
  44. 2∛3
  45. 240y^3+96y^2
  46. p-q
  47. a^2+2ab+b^2
  48. {1, 2, 3, 4, 5, ....}
  49. 16x^3+58x^2+22
  50. -18z^2+6z
  51. Index
  52. Rational
  53. x^2+z^2+2xz-1
  54. -3<x
  55. 7
  56. {... -3, -2, -1, 0, 1, 2, 3, ...}
  57. Quartic
  58. FOIL
  59. Irrational
  60. “Many”