Domain (-∞, ∞) No Variable Maximum at the vertex f(x)=c No x- intercept Opens upwards Starts at (0,0) Parabola with vertex at origin Domain: [0,∞) f(x)=2^x Horizontal Asymptote Defined for x>0 Range is [0, ∞) Free! Has a point of inflection at the origin Graph passes through (1,0) Has no real roots Symmetry about the y-axis Graph is straight line with slope of 1 f(x)=log(x) f(x)=x^2 Approaches 0 but never touches the x-axis Free! Graph decreases as x approaches zero Straight line through the origin Domain (-∞, ∞) No Variable Maximum at the vertex f(x)=c No x- intercept Opens upwards Starts at (0,0) Parabola with vertex at origin Domain: [0,∞) f(x)=2^x Horizontal Asymptote Defined for x>0 Range is [0, ∞) Free! Has a point of inflection at the origin Graph passes through (1,0) Has no real roots Symmetry about the y-axis Graph is straight line with slope of 1 f(x)=log(x) f(x)=x^2 Approaches 0 but never touches the x-axis Free! Graph decreases as x approaches zero Straight line through the origin
(Print)
Domain (-∞, ∞)
No Variable
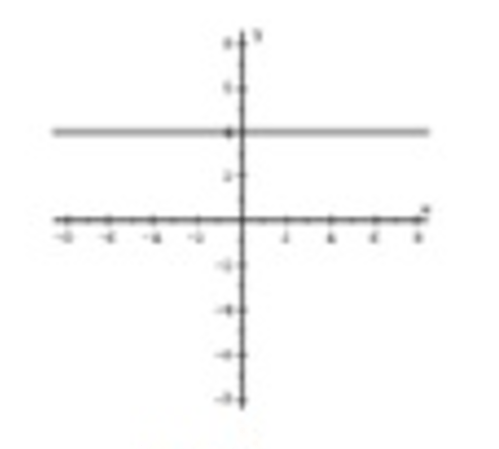
Maximum at the vertex
f(x)=c
No x-intercept
Opens upwards
Starts at (0,0)
Parabola with vertex at origin
Domain: [0,∞)
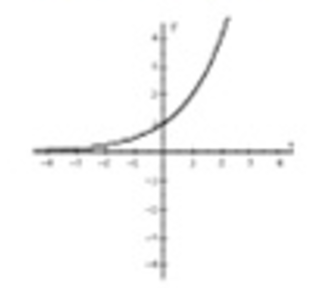
f(x)=2^x
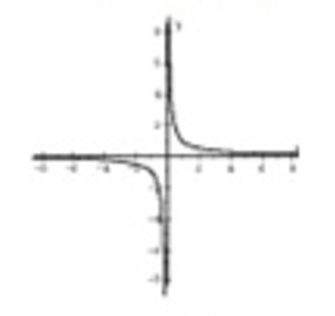
Horizontal Asymptote
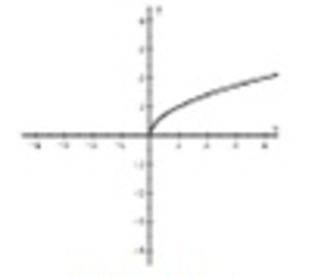
Defined for x>0
Range is [0, ∞)
Free!
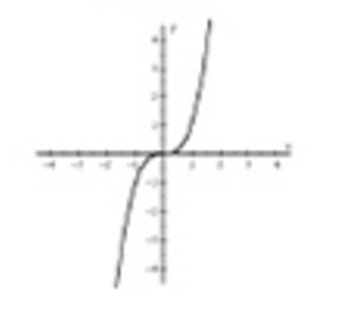
Has a point of inflection at the origin
Graph passes through (1,0)
Has no real roots
Symmetry about the y-axis
Graph is straight line with slope of 1
f(x)=log(x)
f(x)=x^2
Approaches 0 but never touches the x-axis
Free!
Graph decreases as x approaches zero
Straight line through the origin